Tales'theorem

This is the basic theorem of similarities.

The Tales' theorem says: If two straight lines, not necessarily parallel, are cut by a system of parallel lines, then the resultant segments on one of the two lines are proportional to the respective segments obtained on the other line.

A figure to illustrate the above statement:

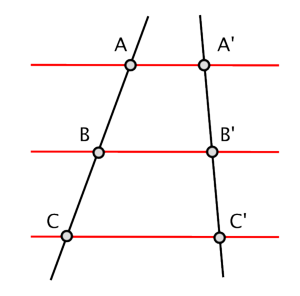
imagen

it is satisfied that $$\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}.$$

For example, given the following figure, decide whether the resultant segments are similar or not.

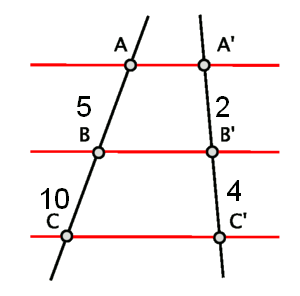
imagen

As we can see in the figure, the segment lengths are as follows: $$(AB = 5, A'B' = 2)$$; $$(BC = 10, B'C' = 4)$$. By Tales'theorem, we can say that the segments among straight lines are similar because the ratios are equal:

$$$\dfrac{AB}{A'B'}=\dfrac{5}{2}=\dfrac{10}{4}=\dfrac{BC}{B'C'}$$$

Finally, we give an application that can be useful for solving certain exercises. Thanks to Tales' Theorem, we can calculate the height of an object, for example, a tree, by the following mechanism.

  1. Let $$C$$ be the length of the shadow of the tree at a certain time.
  2. Let $$B$$ be the length of the shadow of a small object, for example a pencil, at the same instant.
  3. Let $$A$$ be the height of the pencil.

Then, it is satisfied that the height of the tree, called $$H$$, is given by the following equation: $$$H=C\cdot\Big(\dfrac{A}{B}\Big)$$$