A system of equations is non-linear if at least one of its equations is not linear (there is some exponent which is greater than one).
These systems will usually be solved by replacement. When possible, it is advisable to draw the equations of the system in order to have an approximate idea of the possible solutions.
Find the solutions, if there are any, to $$$\left\{ \begin{array}{c} x^2+y^2=25 \\ x+y=5 \end{array} \right.$$$
As has been said, it turns out to be useful to draw the functions. Still, without drawing them, we can see that the first equation is that of a circumference centred on $$(0,0)$$ and of radius $$5$$. Then, three situations could happen:
- No solution exists: The straight line runs above or below the circumference without cutting it.
- Only one solution exists: The straight line is tangent to the circumference.
- Two solutions exist: The straight line cuts the circumference twice.
In the proposed example we can see that there will be two solutions:
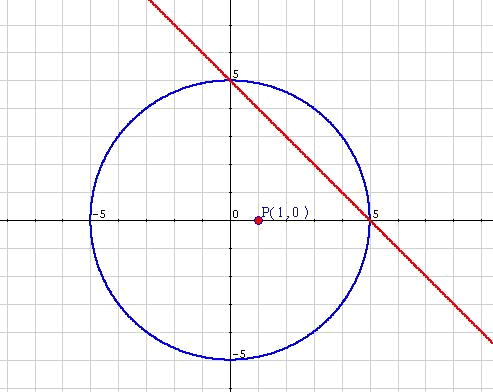
Analytical resolution:
1) We obtain one variable in terms of the other by using one of the equations (it will be easier to start with the linear one) $$$y=5-x$$$
2) We then replace it in the other equation: $$$x^2+(5-x)^2=25$$$
3) We solve: $$$x^2+25-10x+x^2=25 \\ 2x^2-10x=0 \\ x\cdot(2x-10)=0 \\ x_1=0 \\ 2x-10=0 \rightarrow x_2=5$$$
4) And, substituting back into the other equation, $$$x_1=0 \Rightarrow y_1=5$$$ $$$x_2=5 \Rightarrow y_2=0$$$
Note that what we observed in the graphic is what we have seen throughout the analytic approach.
We have to insist on the need to try to imagine the graphic representation before solving the exercise. This will allow us a solution focused on a result, which is always more effective than solving the system without any approximate idea of what will be obtained.
