An ellipse is defined as the geometric place of the points of the plane which sum of distances to two fixed points called foci is constant. Its graphic representation is:
Now we are going to define the elements that characterize it.
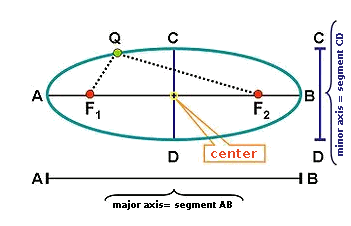
- Foci: the fixed points $$F_1$$ and $$F_2$$.
- Focal axis: it is the straight line that passes two foci.
- Secondary axis: it is the mediator of the segment formed by two foci.
- Center: it is the point of intersection of the focal axis with the secondary axis.
- Focal distance: it is the distance between two foci. The focal semidistance is then the half and therefore the distance of any focus to the center (which we call $$c$$).
- Apexes: it is the cutting point of the ellipse with the secondary and focal axes.
- Major axis: it is the segment that joins the apex $$A$$ with the apex $$B$$.
- Minor axis: it is the segment that joins the apex $$C$$ with the apex $$D$$.
- Symmetry axes: the straight lines that contain some of two following axes: the biggest or the minor.
- Center of symmetry: it coincides with the center of the ellipse and it is the point of intersection of all the axes of symmetry.
The eccentricity of an ellipse (it is denoted by the letter $$e$$) is the ratio between its focal semidistance and its biggest semiaxis.
This value is between zero and one since $$a>c>0$$. So it is: $$$\displaystyle e=\frac{c}{a}$$$ where $$c$$ is the focal semidistance and to $$a$$ is the length of the biggest semiaxis.
The eccentricity indicates the form of an ellipse, that's why an ellipse will be more rounded as its eccentricity nears the value zero. And more flattened the closer the value is to $$1$$.
$$c=0$$, $$b=a$$; Eccentricity $$e=0$$
$$c=3$$, $$a=5$$; Eccentricity $$\displaystyle e=\frac{3}{5}$$
$$c=4$$, $$a=5$$; Eccentricity $$\displaystyle e=\frac{4}{5}$$
$$c=a$$, $$b=0$$; Eccentricity $$e=1$$




