In a less strict way we can define the side continuity, from the left and from the right.
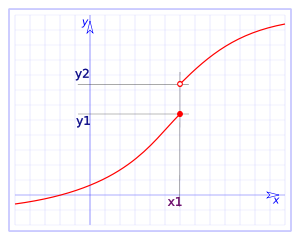
A function is continuous in the point $$x=a$$ from the right if: $$$\displaystyle \lim_{x \to a^+}f(x)=f(a)$$$ and we say that it is continuous in the point $$x=a$$ from the left if: $$$\displaystyle \lim_{x \to a^-}f(x)=f(a)$$$ We can see next an example of continuous function from the left but not from the right at the point $$x=1$$
Let's see a few examples to better understand the concept:
Let's take the function $$\displaystyle f(x)=\left\{\begin{array}{rcl} x & \mbox{ if } & x < 1 \\ -x & \mbox{ if } & x \geq 1 \end{array}\right.$$ and let's study the side continuity at $$x=1$$:
Side continuity from the right: $$$\displaystyle \lim_{x \to 1^+}f(x)=\lim_{x \to 1} -x= -1$$$ and the function at $$x=1$$ takes the value $$f(1)=-1$$, therefore the function is continuous from the right.
Side continuity from the left: $$$\displaystyle \lim_{x \to 1^-} f(x)=\lim_{x \to 1} x=1$$$ and the function in $$x=1$$ takes the value $$f(1)=-1$$, therefore the function is not continuous from the left.
We observe that the functions that are continuous in a point, are continuous for right and for left, or said the other way round, that when the side continuity coincides for the right and for the left, we say that the function is continuous in the point.
