Now that we can work with complex numbers and the basic operations: sum, subtraction, multiplication and division, we are going look at the representation of the complex numbers on the complex plane. For the real numbers, we were drawing a straight line and placed them in an organized manner, as follows:
To represent a complex number graphically, we have to draw them in the complex plane. This is formed by a real axis and an imaginary axis. On the real axis we will represent the real part of the complex number, while in the imaginary axis we will represent the imaginary part. We will draw the above mentioned axis perpendicular and intersecting at zero, which has real and imaginary parts equal to zero.
Let's see an example of the complex plane:
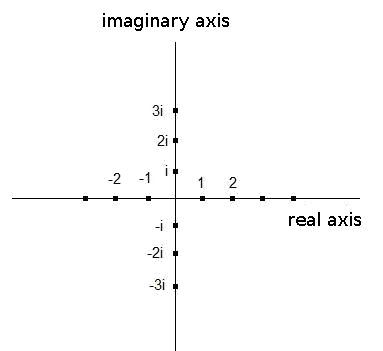
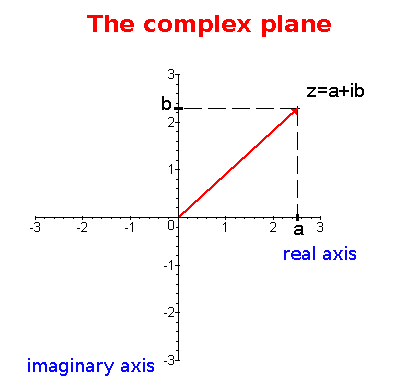
A complex number $$z$$ in binomic form will be represented then in the complex plane in the following form:
We have the complex $$z=a+bi$$ where:
- $$a$$ is any real number, and it is called real part of $$z$$.
- $$b$$ is any real number, and it is called imaginary part of $$z$$.
Then, we represent $$z=a+bi$$ in the plane with the vector associated with $$z$$ which is the vector with origin $$(0,0)$$ and moving towards the point $$(a,b)$$.
We take the real part of the complex number and place it on the real axis. We take the imaginary part and place it on the imaginary axis. We trace two lines parallel to the axis at each of these two points and look for the intersection. The vector pointing to the intersection of these lines is the representation of the complex number $$z$$.
For example, if we want to represent the imaginary number $$z=2-i$$.
First we place $$2$$ in the real axis.
Then we place $$-i$$ in the imaginary axis.
We draw two straight lines:
- one parallel to the real axis in $$-i$$.
-
one parallel to the imaginary axis in the point $$2$$.
The intersection point of these two straight lines is the number $$z$$ that we wanted to represent.
Graphically:
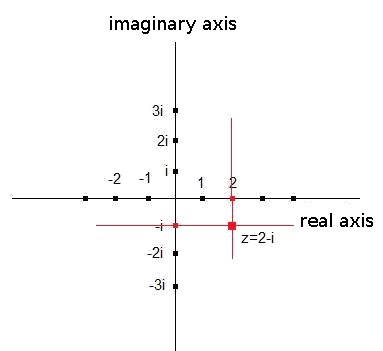
What we are doing is to associate the vector $$(a,b)$$ to the complex number $$z=a+bi$$ in order to graphically represent $$z$$.
For example, the complex number $$3+9i$$ is associated with the vector of the plane $$(3,9)$$ and the complex $$-5i$$ is associated with the vector $$(0,-5)$$.
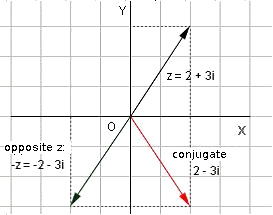
Previously we said that:
We defined the conjugate of an imaginary number as the number $$\bar{z}=a-ib$$. In this case, we will represent it with the associated vector $$(a,-b)$$.
The opposite of an imaginary number is $$z_{op}=-z=-a-bi$$, with associated vector $$(-a,-b)$$.
And the inverse of a complex number is $$z^{-1}=\dfrac{a}{a^2+b^2}-\dfrac{b}{a^2+b^2}i$$ that has the associated vector $$\big(\dfrac{a}{a^2+b^2},-\dfrac{b}{a^2+b^2}\Big)$$.
If we draw them in the complex plane: