Once we understand what position a circle can have regarding other elements on the plane, let see two circles on the plane and the relative position between them.
- Externals, if they do not overlap and the distance between their centers is greater than the sum of their radius. No matter if they have the same or different radius.
Different external circumferences

Equal external circumferences
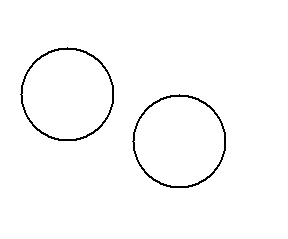
- Externally tangent, if they have just one common point and all other points are exterior to the other. The distance between their centers equals the sum of their radius. No matter whether they have an equal or different radius.
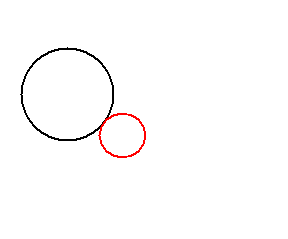
- Secants, if they intersect at two different points and the distance between their centers is less than the sum of their radius. No matter if they have the same or different radius. Two different circles cannot intersect at more than two points. Two intersecting circles are orthogonal if the angle between their tangents at the two contact points is a right angle.
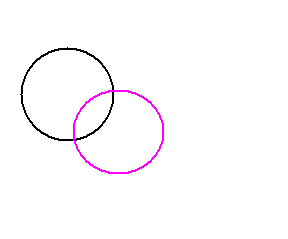
- Internally tangent, if they have a common point and all other points of one of them are interior to the other, exclusively. The distance between their centers is equal to the difference of their radius. One has to have a greater radius than the other.
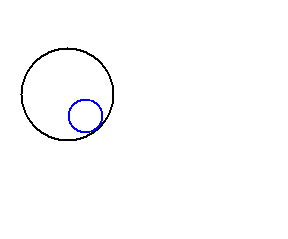
- Eccentric interior, if they have no common points and the distance between their centers is greater than 0 and less than the difference of their radius. One has to have a greater radius than the other.

- Concentric interiors, if they have the same center (the distance between their centers is 0) and a different radius. They form a figure known as annulus or ring. One has to have a greater radius than the other one.

- Overlapping, if they have the same center and the same radius. Actually, these two different circles are the same circle. If two circles intersect at more than two points, they are necessarily overlapping circles.
Note: we do not show any example of this case and the reason why is clear in the definition.
