Let $$C$$ be a curve in the space or on the plane, a parametrization of $$C$$ is a function $$$\gamma:[a,b] \longrightarrow \mathbb{R}^{n}$$$ for $$n=2$$ or $$3$$ (on the plane or in the space), so that for every $$t$$ of the interval $$[a, b]$$, there is a corresponding point of the plane (and only one point) or of the space. This $$\gamma$$ must be a continuous function and must be derivable.
A parametrization of a circle of radius one: $$$\begin{array} {ccc} \gamma: [0,2 \pi] & \longrightarrow & \mathbb {R} ^{n} \\ \theta & \longrightarrow & (\cos \theta, \sin \theta) \end{array}$$$ since for every point $$(x,y)$$ of the circle, there exists some $$\theta$$ , so that $$\gamma(\theta)=(x,y)$$.
A parametrization of an ellipse of semiaxes $$a$$ and $$b$$, $$$ \begin{array} {ccc} \gamma: [0,2 \pi] & \longrightarrow & \mathbb {R} ^{2} \\ \theta & \longrightarrow & (a \cdot \cos \theta, b \cdot \sin \theta) \end{array}$$$
A parametrization of a parabole: $$$\begin{array} {ccc} \gamma: [0,5] & \longrightarrow & \mathbb {R} ^{2} \\ t & \longrightarrow & (t, t^{2}) \end{array}$$$ In general, if we have a function $$f(x)$$ we can parametrize its graph as $$\gamma (x) = (x,f(x))$$.
A parametrization of the segment that joins the point of the plane $$(2,3)$$ with the $$(-1,1)$$ is $$$\begin{array} {ccc} \gamma: [0,1] & \longrightarrow & \mathbb {R} \\ t & \longrightarrow & t \cdot \left(\begin{array}{c} 2 \\ 3 \end{array}\right) + (1-t) \cdot \left( \begin{array}{c} -1 \\ 1\end{array}\right) \end{array}$$$
The parametrization $$$\begin{array} {ccc} \gamma: [0,5] & \longrightarrow & \mathbb {R} ^{3} \\ t & \longrightarrow & (\cos t, \sin t, t) \end{array}$$$ is a spiral. To see it more clearly, it is useful to look at how the graph would be if we were to eliminate one component. If, for example, we remove the third component (looking at the figure from above), we have a circle and the height is increasing, so we have a spiral.
The parametrization of the segment that joins the points of the space $$(0,0,1)$$ and $$(3,2,0)$$ is $$$\begin{array} {ccc} \gamma: [0,1] & \longrightarrow & \mathbb {R} \\ t & \longrightarrow & t \cdot \left(\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right)+(1-t) \cdot \left(\begin{array}{c} 3 \\ 2 \\ 0 \end{array}\right) \end{array}$$$
A parametrization of a circle of radius one,in a flat position at a height of $$z=3$$, is given by the function $$$ \begin{array} {ccc} \gamma: [0,2 \pi] & \longrightarrow & \mathbb {R} ^{3} \\ \theta & \longrightarrow & (\cos \theta, \sin \theta, 3) \end{array}$$$
Considering a curve $$C$$ on the plane or in the space, it is possible to obtain its parametrization $$\gamma$$ in several ways. Sometimes, we will use one of the coordinates as a variable for the parametrization, as in example 3. If we have the function's graph, then this will be used for the parametrization. In other words:
- Let $$f(x)$$ be a continuous and derivable function, then $$\gamma(x)=(x,f(x))$$ is a parametrization of its graph.
But this is not useful, for example, in the case of a circle (example 1), since the circle has, for every $$x$$, two different values of $$y$$. We can however parametrize the top half of the circle.
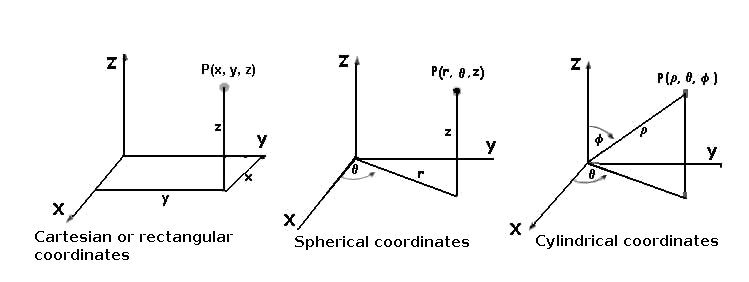
- Another way of obtaining parametrizations of curves is by taking different coordinates systems, such as, for example, the spherical coordinates (radius and 2 angles) or the cylindrical ones (radius, height and angle).