Infinity's comparison

When we know that certain functions tend to infinity, we can ask ourselves if there are some of these functions that tend to infinity faster than others. This indicates that an infinity can be greater than another not because it is greater than the former, but rather because it goes to infinity more rapidly.

A clear example can be the following one:

Let's take the functions $$f(x)=e^x$$ and $$g(x)=\ln x$$.

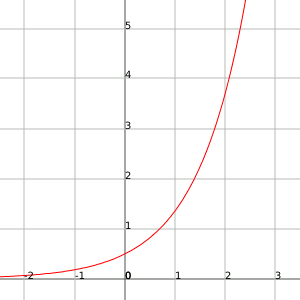
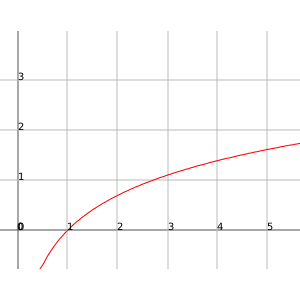
If we represent them graphically we will observe that the exponential function grows very rapidly while the function logarithm has very slow growth. The two reach the infinite, but the exponential function reaches the infinite much more rapidly than the logarithmic one, therefore we say that the infinite of the exponential function is greater than that of the logarithm.

Exponential function:

Function logarithm:

Then, how do we distinguish if a function tends to infinite more quickly than another function?

This question is solved using the division:

Let's suppose that $$\displaystyle\lim_{x \to{+}\infty}{f(x)}= \pm \infty$$ and that $$\displaystyle\lim_{x \to{+}\infty}{g(x)}=\pm \infty$$.

We say that the infinite of $$f(x)$$ is an infinite of higher order than $$g(x)$$ if:

$$$\displaystyle\lim_{x \to{+}\infty}{\frac{f(x)}{g(x)}}= \pm \infty$$$

or equivalently if:

$$$\displaystyle\lim_{x \to{+}\infty}{\frac{g(x)}{f(x)}}=0$$$

In case that:

$$$\displaystyle\lim_{x \to{+}\infty}{\frac{f(x)}{g(x)}=k}$$$

where $$k$$ is a real value, we say that the infinities of the two functions are equivalent or of the same order.

Let's see the behavior of the powers, the exponential and the logarithm:

• Given two powers of $$x$$, that of higher power has an infinite of higher order: if

$$$n>k \Rightarrow \displaystyle\lim_{x \to{+}\infty}{\frac{x^n}{x^k}}=\displaystyle\lim_{x \to{+}\infty}{x^{n-k}}=+\infty$$$

where $$n$$ and $$k$$ can be positive real values.

In case of having the same exponent we will obtain that:

$$$\displaystyle\lim_{x \to{+}\infty}{\frac{ax^n}{b^n}}=\displaystyle\lim_{x \to{+}\infty}{\frac{a}{b}}=\frac{a}{b}$$$

Therefore, if we have to find limit of the division between two polynomials, and since we know that the infinity of a polynomial is driven by its highest power, we will be able to find the limit by looking only at the highest power in each of the two polynomials.

Let's see some examples:

• Given two exponential functions whose base is greater than 1, we will have that the one with greater base will be also the one with an infinite of higher order, if $$a>b>0$$ then:

$$$\displaystyle\lim_{x \to{+}\infty}{\frac{a^x}{b^x}}=+\infty$$$

Let's see some examples:

Also, any exponential function whose base is greater than $$1$$ is an infinite of order superior to any power, if:

$$a>1$$ and $$n<0$$ then $$$\displaystyle\lim_{x \to{+}\infty}{\frac{a^x}{x^n}}=+ \infty$$$

Let's see some examples:

• Given two logarithmic functions whose base is greater than $$1$$, the corresponding infinites are always equivalent (or of the same order).

This means that if $$a>1$$ and $$b>1$$ then:

$$$\displaystyle\lim_{x \to{+}\infty}{\frac{\log_{a} x}{\log_{b}x}}=k$$$

where $$k$$ is a real value.

And also, any power function is an infinite of higher order than any logarithmic function (and consequently any exponential function as well).

• We end up by mentioning that if in a sum there are several types of infinity, the order of the sum is that of the highest order of its elements: