Euclidian distance

Euclidian distance

The absolute value allows to define the distance between two real numbers.

Given two numbers $$a$$ and $$b$$, they determine two points on the real line, which we denote by $$A$$ and $$B$$. We define the distance between $$a$$ and $$b$$ as the length of the segment $$AB$$.

Let's see the different cases that we can find:

1. $$0 < a < b$$: in this case, both numbers are on the right of zero. Then, the length of the segment is calculated doing: $$$AB=0B-0A=b-a=|b-a|$$$

As we can see in the figure:

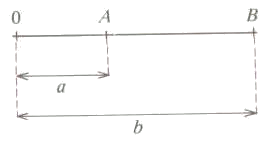
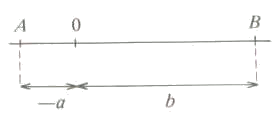
2. $$a < b < 0$$: in this case, both numbers are on the left of zero. Then, the length of the segment is calculated by doing $$$AB=0A-0B=-a-(-b)=a-b=-(b-a)=|b-a|$$$ Graphically:

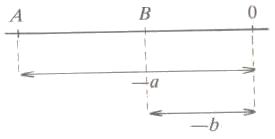
3. $$a < 0 < b$$: in this case we have one number on the right and another on the left of zero. In this case we have that the length of the segment is $$$AB=A0+0B=-a+b=-(b-a)=|b-a|$$$ Or graphically:

In general, we can say that the distance between two numbers $$a$$ and $$b$$, is the absolute value of its difference, and we will denote it by: $$$d(a,b)=|b-a|$$$

Properties of the Euclidian distance

As consequences of the properties of the absolute value we see that, considering three real numbers $$a,b$$ and $$c$$, it is satisfied that

• $$d(a,b)>0$$; and $$d(a,b)=0$$ if and only if $$a=b$$.
• $$d(a,b)=d(b,a)$$.
• $$d(a,b) \leq d(a,c) + d(c,b)$$

The absolute value and the distance defined previously are named as Euclidean norm and Euclidean distance, respectively. These represent the most intuitive distance concept on the real line.