Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. A la distancia se le denomina radio.
Esta propiedad es la clave para hallar la expresión analítica de una circunferencia.
Veamos como:
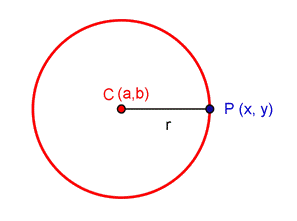
Una circunferencia de centro $$C = ( a, b)$$ y radio $$r$$, está formada por todos los puntos $$P = (x, y)$$ cuya distancia al centro es $$ r$$.
Expresando esto en forma de ecuación matemática tenemos: $$$\displaystyle d(C,P)=d((a,b),(x,y))= \sqrt{(x-a)^2+(y-b)^2} =r$$$ Elevando al cuadrado esta ecuación obtenemos la ecuación reducida de la circunferencia: $$$ \displaystyle d(C,P)^2=\Big( \sqrt{(x-a)^2+(y-b)^2} \Big)^2=(x-a)^2+(y-b)^2=r^2$$$ Por lo que cualquier expresión del tipo $$$(x-a)^2+(y-b)^2=r^2$$$ es una circunferencia de radio $$r$$ y centro el punto $$(a, b)$$.
$$ (x-1)^2+(y-2)^2=3^2$$ es una circunferencia de radio $$3$$ y centrada en el punto $$(1, 2)$$.
Cuando consideramos una circunferencia centrada en el origen, estamos cogiendo $$C = (0, 0)$$ y por lo tanto la ecuación es $$x^2+y^2=r^2$$.
$$x^2+y^2=4^2$$ está centrada en el origen y tiene radio $$4$$.
La circunferencia con centro en el origen y radio 1 se llama circunferencia unidad.
Si por ejemplo queremos escribir la ecuación de una circunferencia centrada en el punto $$(-8, 0)$$ y con diámetro $$36$$, el procedimiento es:
Calculamos el radio: $$$\displaystyle r=\frac{\mbox{diameter}}{2}=\frac{36}{2}=18$$$
Sustituimos los parámetros en la ecuación de la circunferencia, con $$r=18$$ y $$C = (-8, 0)$$: $$$\displaystyle (x-(-8)^2)+(y-0)^2=18^2 \Rightarrow (x+8)^2+y^2=18^2$$$ Y ya tenemos la ecuación.
