We will call the circumference: the geometric locus of points on the plane that are equidistant to a fixed point called center. This distance is named radius.
This property is the key to finding the analytical expression of a circumference.
Let's see it:
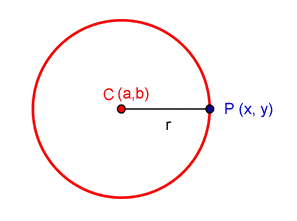
A circumference of center $$C = ( a, b)$$ and radius $$r$$, is formed by all the points $$P = (x, y)$$ whose distance to the center is $$ r$$.
Expressing this in a mathematical equation we have: $$$\displaystyle d(C,P)=d((a,b),(x,y))= \sqrt{(x-a)^2+(y-b)^2} =r$$$ Squaring this equation we obtain the reduced equation of the circumference: $$$ \displaystyle d(C,P)^2=\Big( \sqrt{(x-a)^2+(y-b)^2} \Big)^2=(x-a)^2+(y-b)^2=r^2$$$ For which reason, any expression of the type $$$(x-a)^2+(y-b)^2=r^2$$$ is a circumference of radius $$r$$ and center at the point $$(a, b)$$.
$$ (x-1)^2+(y-2)^2=3^2$$ is a circumference of radius $$3$$ and centred at the point $$(1, 2)$$.
When we consider a circumference centred on the origin, we are taking $$C = (0, 0)$$ and therefore the equation is $$x^2+y^2=r^2$$.
$$x^2+y^2=4^2$$ it is centred on the origin and has a radius of $$4$$.
The circumference with center in the origin and radius $$1$$ is called a unit circumference.
If, for example, we want to write the equation of a circumference centred at point $$(-8, 0)$$ and with diameter $$36$$, the procedure is:
We calculate the radius: $$$\displaystyle r=\frac{\mbox{diameter}}{2}=\frac{36}{2}=18$$$
We replace the parameters in the equation of the circumference, with $$r=18$$ and $$C = (-8, 0)$$: $$$\displaystyle (x-(-8)^2)+(y-0)^2=18^2 \Rightarrow (x+8)^2+y^2=18^2$$$ So we already have the equation.
