Sabem que la derivada d'una funció d'una variable en un punt ens dóna el pendent de la recta tangent a la funció en aquest punt. Això vol dir que sabem la rapidesa de creixement/decreixement de la funció en aquest punt.
Ara suposem que tenim una funció $$f$$ que depèn de més d'una variable, per exemple $$f(x,y)=-x^2+2xy-y$$.
En ser una funció de dues variables, la gràfica és una superfície, i per tant hi ha infinites direccions entre les que podem estudiar el creixement.
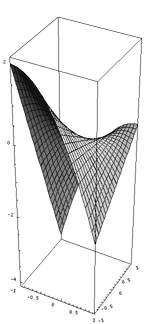
Doncs bé, les derivades parcials ens indicaran també el pendent d'una recta concreta tangent a la superfície. Abans, però, aprendrem a calcular derivades parcials, ja que és un metodologia a la que després donarem sentit.
Per calcular una derivada parcial d'una funció en diverses variables, hem de derivar com sempre respecte una de les variables i mantenir les altres com a constants, (com a valors fixos).
En el nostre exemple $$f(x,y)=-x^2+2xy-y$$, si volem fer la derivada parcial respecte $$x$$, considerem la variable $$y$$ com una constant, "un nombre", i el que queda serà com derivar una funció d'una variable, $$f(x)$$. Vegem-ho:
$$-x^2$$ només depèn de $$x$$; per tant, la seva derivada és $$-2x$$.
$$2xy$$ conté la variable $$y$$, però és como si fos una constant, un nombre. Si fos un $$3$$ faríem $$2x3=6x$$, i la derivada seria $$6$$. Doncs ara escric $$2xy$$ com a $$2yx$$ i considero $$2y$$ com si fos el $$6$$. Per tant, la derivada de $$2xy=2yx$$ és $$2y$$.
I finalment, $$y$$ no conté la variable $$x$$, i la derivada d'una constant és $$0$$. Per tant, desapareix.
Ara només ens falta saber la notació per poder escriure-ho matemàticament. Per a la derivada parcial d'una funció $$f$$ respecte la variable $$x$$, podem trobar les notacions:
$$$\dfrac{\delta f}{\delta x}$$$ $$$\delta_x f$$$ $$$f_x$$$
Així, la nostra derivada parcial respecte $$x$$ de $$f(x,y)=-x^2+2xy-y$$ s'escriu
$$$\dfrac{\delta f}{\delta x}=-2x+2y-0=2x+2y$$$ $$$\delta_x f=-2x+2y$$$ $$$f_x=-2x+2y$$$
I ara us preguntareu: També podem fer la derivada parcial respecte $$y$$, no? Doncs clar que sí.
Fem el càlcul de $$\dfrac{\delta f}{\delta y}$$, amb el qual ens imaginem que $$x$$ és una constant.
$$-x^2$$ no conté la variable $$y$$, i com abans, és com si tinguéssim simplement una constant. La seva derivada és $$0$$.
$$2xy$$ conté la variable $$x$$, però és com si fos una constant, un nombre. Per tant, la derivada de $$2xy$$ és $$2x$$.
I finalment, com que estem derivant respecte $$y$$, la derivada de $$y$$ és $$1$$.
Així, $$$\dfrac{\delta f}{\delta y}=\delta_y f=f_y=2x-1$$$
Interpretació geomètrica de la derivada parcial
Però què significa geomètricament el càlcul d'una derivada parcial? Vegem el següent exemple:
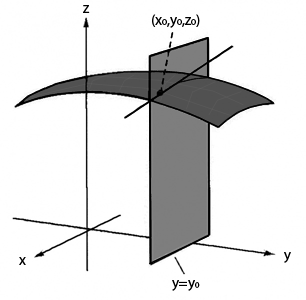
En aquest gràfic tenim una superfície $$z=f(x,y)$$ de la qual estem fent la derivada parcial respecte la variable $$x$$ en un punt $$x_0,y_0,z_0$$. Hem vist que fer la parcial respecte $$x$$ significa deixar la variable $$y$$ com a constant. Mantenir el valor fix $$y=y_0$$ ens dóna com a resultat un pla que passa pel punt $$y_0$$. Construïm llavors el pla que sigui paral·lel a l'eix $$x$$. Aquest pla talla la nostra superfície. A la corba intersecció considerem la recta tangent en el punt $$x_0,y_0,z_0$$. La derivada parcial ens donarà el pendent d'aquesta recta.
Si en la nostra funció d'exemple $$f(x,y)=-x^2+2xy-y$$ volem el valor del pendent de la recta tangent a la superfície en el punt $$3,1$$ en la direcció de l'eix $$x$$, ens queda
$$$\dfrac{\delta f}{\delta x}=-2x+2y$$$ $$$\dfrac{\delta f(3,1)}{\delta x}=(-2)·3+2·1=-6+2=-4$$$
En una funció $$z=f(x,y)$$, la derivada parcial respecte $$y$$ es representaria gràficament seguint l'exemple gràfic:
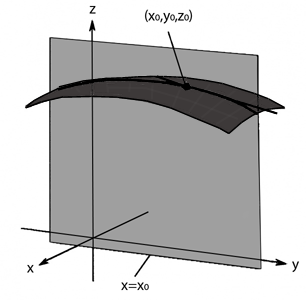
Ara el valor constant és $$x=x_0$$, i el pla és paral·lel a l'eix $$y$$.
En la nostra funció d'exemple, si volem saber el pendent en la direcció $$y$$ en el punt $$(0,1)$$, obtenim
$$$\dfrac{\delta f}{\delta y}=2x-1$$$ $$$\dfrac{\delta f(0,1)}{\delta y}=-1$$$
i veiem que la inclinació de la superfície en aquest punt i en la direcció ja comentada és descendent.
En definitiva, que quan calculem les derivades parcials $$\dfrac{\delta f}{\delta x}$$ o $$\dfrac{\delta f}{\delta y}$$ en el punt $$x_0,y_0,z_0$$, el valor que obtenim és el pendent de la superfície en la direcció de l'eix $$x$$ o de l'eix $$y$$, respectivament.
Definició formal de derivada parcial
La definició formal de derivada parcial segueix sent el càlcul d'un límit, com amb la derivada d'una funció d'una variable.
Sigui $$U$$ un subconjunt obert de $$\mathbb{R}^n$$ i una funció $$f: \ U \rightarrow R$$. Definim la derivada parcial de $$f$$ en el punt $$p\in U$$, $$p=p_1,...,p_n$$, respecte la variable $$x_i$$ com a
$$$\dfrac{\delta f(p)}{\delta x_i}=\lim_{h\rightarrow 0}\dfrac{f(p_1,...,p_{i-1},p_i+h,p_{i+1},...,p_n)-f(p_1,...,p_n)}{h}$$$
Exemples de càlcul de derivades parcials
Per a una bona realització s'han de tenir presents dues coses: les regles de derivació en una variable i saber imaginar-nos com a constants les variables que corresponguin en cada cas. Veuràs com és qüestió de pràctica.
Donada la funció $$f(x,y)=\sqrt{x^3+y^2}$$, calcula $$f_x(1,1)$$.
Reescric $$f(x,y)=(x^3+y^2)^{\frac{1}{2}}$$ com ho fèiem per derivar arrels quan només hi havia una variable. Ara pensem en $$y$$ com una constant i derivem fent servir les regles habituals:
$$$f_x=\dfrac{1}{2}(x^3+y^2)^{-\frac{1}{2}}\cdot3x^2=\dfrac{3x^2}{2\sqrt{x^3+y^2}}$$$
Per saber el pendent en el punt $$(1,1)$$, substituïm
$$$f_x (1,1)=\dfrac{3}{2\sqrt{2}}$$$
Donada la funció $$f(x,y)=\dfrac{2xy-y}{x^2+y}$$, calcula la derivada parcial respecte $$x$$ i $$y$$.
$$$\dfrac{\delta f}{\delta x}=\dfrac{2y(x^2+y)-(2xy-y)2x}{(x^2+y)^2}=\dfrac{2yx^2+2y^2-4x^2y+2xy}{(x^2+y)^2}=\dfrac{-2x^2y+2xy+2y^2}{(x^2+y)^2}=\dfrac{2(-x^2y+xy+y^2)}{(x^2+y)^2}$$$
$$$\dfrac{\delta f}{\delta y}=\dfrac{(2x-1)(x^2+y)-(2xy-y)}{(x^2+y)^2}=\dfrac{2x^3+2xy-x^2-y-2xy+y}{(x^2+y)^2}=\dfrac{2x^3-x^2}{(x^2+y)^2}$$$
Donada la funció $$f(x,y,z)=x^2y^3-2xyz^3$$, calcula el pendent de la recta tangent al punt $$(1,-1,1)$$ en les direccions dels eixos $$x$$, $$y$$ i $$z$$.
$$$\dfrac{\delta f}{\delta x}=2xy^3-2yz^3$$$ $$$\dfrac{\delta f(1,-1,1)}{\delta x}=2\cdot1\cdot(-1)^3-2\cdot(-1)\cdot1^3=0$$$
$$$\dfrac{\delta f}{\delta y}=3x^2y^2-2xz^3$$$ $$$\dfrac{\delta f(1,-1,1)}{\delta y}=3-2=1$$$
$$$\dfrac{\delta f}{\delta z}=-6xyz^2$$$ $$$\dfrac{\delta f(1,-1,1)}{\delta z}=6$$$
Donada la funció $$f(x,y,z)=\dfrac{2z}{y+\sin(x)}$$ calcula les derivades parcials respecte $$x$$, $$y$$ i $$z$$.
$$$\dfrac{\delta f}{\delta x}=\dfrac{-2z\cos(x)}{(y+\sin(x))^2}$$$
$$$\dfrac{\delta f}{\delta y}=\dfrac{-2z}{(y+\sin(x))^2}$$$
$$$\dfrac{\delta f}{\delta z}=\dfrac{2(y+\sin(x))-2z\cdot0}{(y+\sin(x))^2}=\dfrac{2(y+\sin(x))}{(y+\sin(x))^2}=\dfrac{2}{y+\sin(x)}$$$
Més aplicacions de la derivada parcial
Arribats en aquest punt, potser has pensat en alguna altra informació que podrien proporcionar les derivades parcials. I és que també podem interpretar que la derivada parcial mesura la rapidesa de canvi de la variable que derivem respecte a la variable que deixem fixa. Així podem mesurar com canvia $$y$$ quan deixem $$x$$ fixa i al revés. Vegem un exemple.
Imaginem una placa solar rectangular tal que en zones diferents absorbeix quantitats diferents de llum solar i per tant cada cèl·lula produeix una quantitat diferent d'energia. Tenim una relació tal que, en un punt $$(x,y)$$ de la placa, la potència d'energia generada la podem deduir amb la relació $$$E(x,y)= \dfrac{3}{10}xy + y$$$
Les unitats de $$x$$ i $$y$$ són centímetres i la potència d'energia $$E$$ es mesura en watts. ¿Com varia la potència energètica $$E$$ en el centre de la placa, $$(65,120)$$, quan $$x$$ roman fixa en els $$65$$ cm?
Per saber-ho hem de calcular $$E_y(65,120)$$. $$$E_y=\dfrac{3}{10}x+1 \Rightarrow E_y(65,120)=20,5$$$
Així sabem que situats sobre el punt $$x=65$$, $$y=120$$ la potència energètica augmenta a mesura que avancem en la direcció de l'eix $$y$$, ja que la derivada parcial en aquesta direcció és positiva. A més, la potència energètica generada augmentarà amb una rapidesa de $$20,5$$ W.

