Vamos a aprender a determinar la zona del plano en que se cumplen un conjunto de restricciones (inecuaciones) y a obtener los valores de las coordenadas de los vértices de diche zona.
Normalmente en los ejercicios con inecuaciones se tiene más de una restricción simultáneamente sobre las variables. Por ejemplo, si tenemos como problema el número de sillas (de $$10$$ kg) y mesas (de $$20$$ kg) que puede transportar un camión (que sólo puede llevar como máximo $$1000$$ kg), se tiene que tener en cuenta la restricción de que tanto el número de sillas como el de mesas ha de ser positivo. Por lo tanto , además de la restricción sobre el peso que puede transportar el camión:
(i) $$10\cdot x+20\cdot y\leqslant 1000$$
se tendrán también las restricciones de que tanto el número de sillas ($$x$$) como el número de mesas ($$y$$) han de ser positivos:
(ii) $$x\geqslant0$$
(iii) $$y\geqslant0$$
Cada una de estas restricciones tiene asociada una recta en el plano XY, que separa el plano en dos regiones: la región de validez (región en que se cumple la restricción) y la zona en que no se cumple. A continuación se presentan estas rectas y zonas de validez para las tres restricciones:
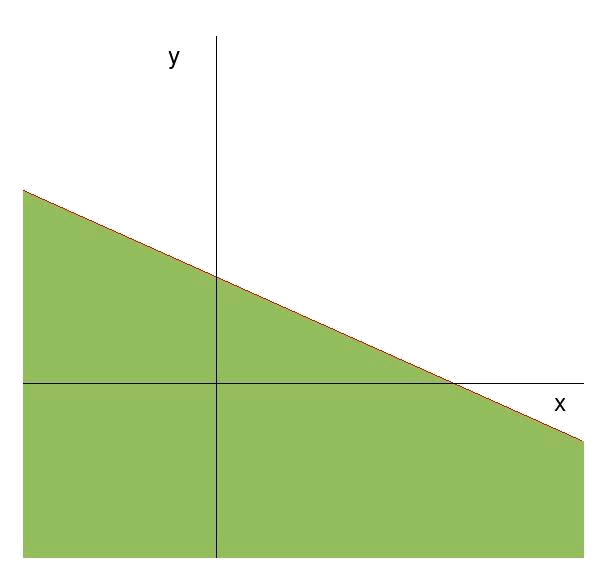
(i) La restricción es: $$$10\cdot x+20\cdot y\leqslant 1000$$$
y por lo tanto la recta asociada es: $$$ f(x)=-\dfrac{1}{2}\cdot x+50$$$
Además si probamos el punto $$(x=0,y=0)$$ en la inecuación: $$$10\cdot 0+20\cdot 0\leqslant 1000$$$
por lo tanto la región de validez será la que contenga el punto $$(0,0)$$:
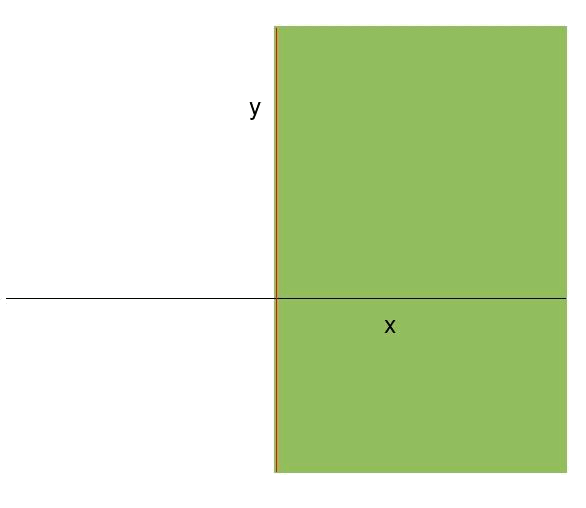
(ii) La restricción es: $$$x\geqslant0$$$
Este tipo de restricción representa una recta vertical (paralela al eje $$y$$) que separa los valores de $$x$$ mayores y menores que $$0$$ respectivamente. La zona de validez serán los valores de $$x$$ mayores que cero:
iii) La restricción es: $$$y\geqslant0$$$
La recta asociada a esta restricción es: $$$g(x)=0$$$
y la zona de validez es, evidentemente, la región por encima de $$g(x)$$, $$\ y\geqslant0$$:

Ahora sería cuestión de conocer la región del plano XY en que se cumplen todas las restricciones simultáneamente. Esta región será la que sea común a las regiones de validez de todas las restricciones. Para el caso de las sillas y las mesas será el triángulo que forman la recta $$f(x)$$ y los ejes $$x$$ e $$y$$:
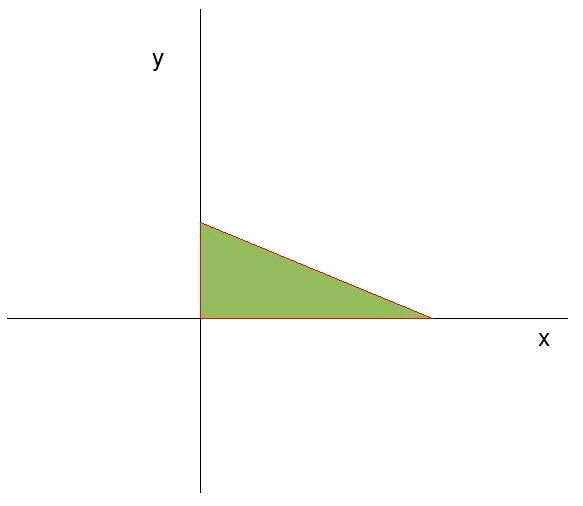
Vemos que en este caso, al tener en cuenta todas las restricciones a la vez, la región de validez (a partir de ahora se referirá a la región común de todas las zonas de validez de las distintas restricciones como región de validez a secas) es una zona acotada del plano. En los ejemplos anteriores la región de validez se extendía por algún lado hasta el infinito, por eso no estaban acotadas esas zonas.
Para conocer bien la región de validez se han de conocer las coordenadas de sus vértices. En este caso es muy sencillo. Ya conocemos las coordenadas de uno de los puntos: el $$(0,0)$$. Los otros dos puntos de corte son los puntos donde la recta $$f(x)$$ corta los ejes.
Los puntos de corte con los ejes se pueden encontrar fácilmente:
-
Para el punto de corte con el eje $$y$$, tan solo se ha de saber que todo el eje $$y$$ tiene coordenada $$x=0$$, y el valor de $$y$$ en el punto de corte será el que tome la función $$f(x)=-\dfrac{1}{2}\cdot x+50$$ en $$x=0$$ (sobre el eje $$y$$). Así pues el punto de corte será: $$(x=0,y=f(0)=50)$$.
- El punto de corte con el eje $$x$$ se da cuando $$y = 0$$, es decir, en el valor de $$x$$ en que la función toma el valor $$0$$: $$$ f(x)=0 \Rightarrow -\dfrac{1}{2}\cdot x+50=0 \Rightarrow x=100$$$ Por lo tanto el punto en que la recta $$f(x)$$ corta el eje $$x$$ es el $$(x=100,y=0)$$.
Así pues los vértices de la región de validez tienen por coordenadas: $$$ (0,0) \quad (0,50) \quad (100,0)$$$
En este caso ha sido muy facil encontrar los vértices.
El siguiente ejemplo ilustrará la forma más general para encontrar los vértices de la región de validez.
Se tienen las siguientes restricciones: $$$\begin{array}{rcl} x+4 &\geqslant& 4 \\ y &\leqslant& 4 \\ y &\geqslant& x \end{array}$$$
que tienen por rectas asociadas: $$$\begin{array}{l} r(x): \ y=-x+4 \\ s(x):\ y=4 \\ t(x):\ y=x \end{array} $$$
Podemos visualizar estas rectas y determinar los semiplanos donde se cumple cada inecuación por separado.
Para la recta $$r$$:
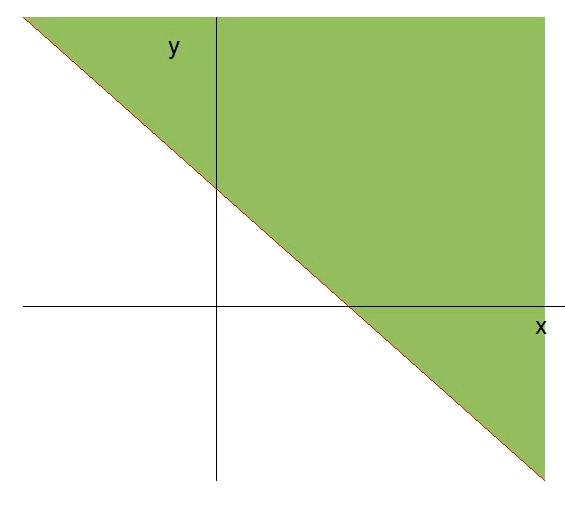
Como no se cumple la inecuación en el punto $$(0,0)$$, $$\ 0+0\ngeqslant 4$$, vemos que la zona de validez de la inecuación és el semiplano por encima de la recta.
Para la recta $$s$$:
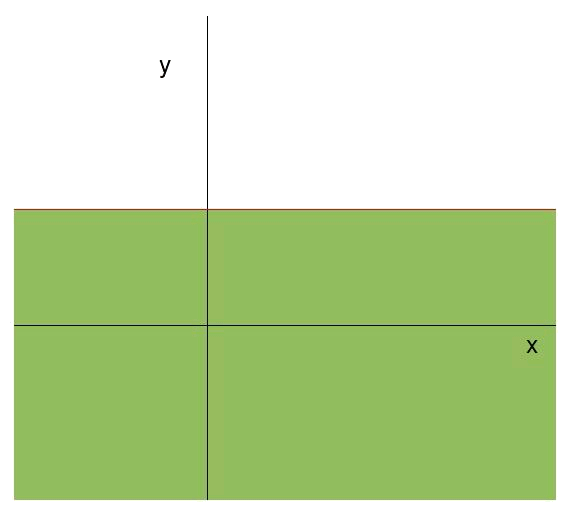
Como se cumple la inecuación en el punto $$(0,0)$$, $$\ 0\leqslant 4$$, vemos que la zona de validez de la inecuación és el semiplano por debajo de la recta.
Para la recta $$t$$:
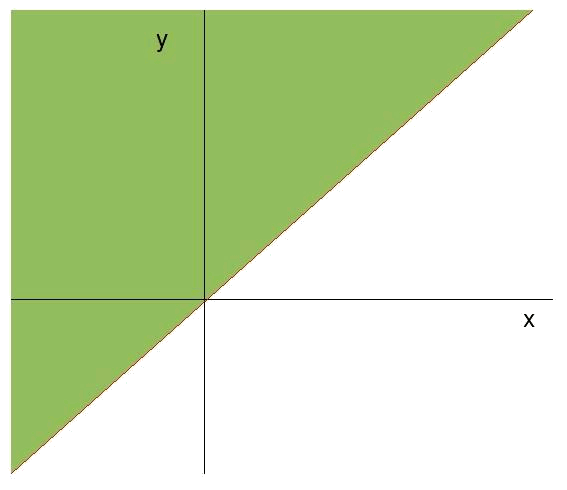
Como se cumple la inecuación en el punto $$(0,1)$$, $$\ 1\geqslant 0$$ vemos que la zona de validez de la inecuación és el semiplano por encima de la recta.
En conjunto tenemos pues:
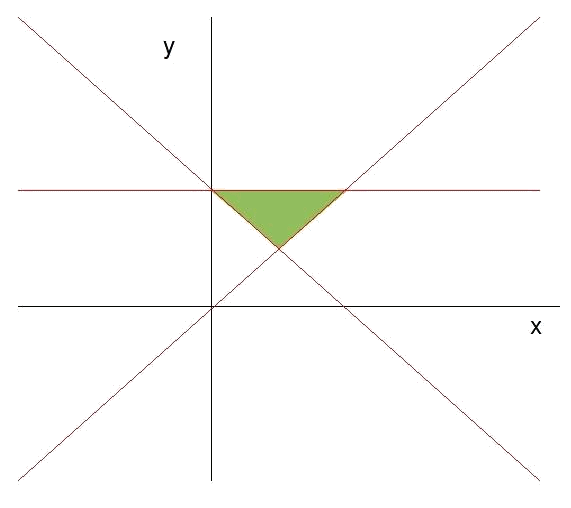
La zona donde coinciden todos los semiplanos es la región factible. Vemos que en este caso se trata también de una zona acotada.
Se ha de realizar ahora el cálculo de los vértices de esta zona. Para ello se necesitará saber el punto en que se cortan las rectas dos a dos. Tendremos que encontrar tres puntos de corte: el de la recta $$r$$ con la $$s$$, la $$r$$ con la $$t$$ y la $$s$$ con la $$t$$.
Cómo hallar el punto de corte de dos rectas:
Conocer un punto significa saber las coordenadas $$x$$ e $$y$$ de dicho punto. Si dos rectas $$f(x)$$ y $$g(x)$$ se cortan, sabemos que ambas funciones estarán tomando el mismo valor en la posición en que se cortan. Gráficamente es:
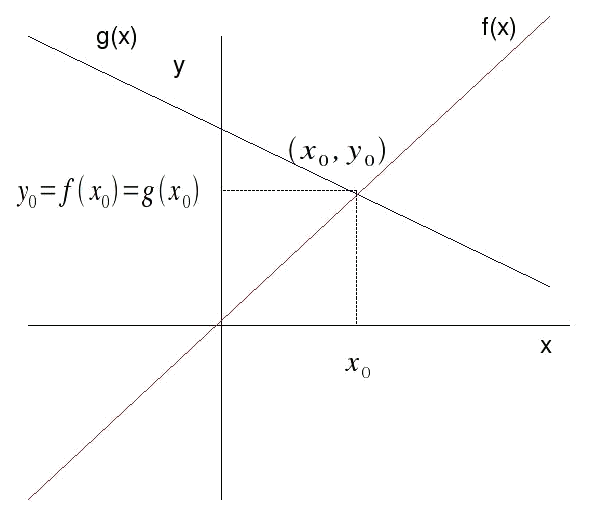
Por lo tanto sabemos que el punto de corta será $$(x_0,y_0)$$ y que el valor de $$y_0$$ es igual al valor de las dos funciones en $$x_0$$, ya que sabemos que las dos funciones tienen que tomar el mismo valor en ese punto para cortarse: $$$ f(x_0)=g(x_0) $$$
Volviendo al ejemplo.
Punto de corte entre $$r$$ y $$s$$:
Se han de encontrar las coordenadas $$x$$ e $$y$$ del punto de intersección. A las coordenadas de este punto les llamaremos $$x_0$$ e $$y_0$$.
Para encontrar la coordenada $$x$$ en que se cortan las rectas, $$x_0$$, igualamos las dos funciones $$r(x)=-x+4$$ y $$s(x)=4$$ en el punto en que se cortan las rectas ($$x_0$$):
$$$ r(x_0)=s(x_0) \Rightarrow -x_0+4=4 \Rightarrow x_0=0$$$
Por lo tanto las dos rectas se cortan en $$x_0=0$$.
Determinar la coordenada $$y$$ del punto de corte, $$y_0$$ es sencillo, pues es el valor que toman tanto la función $$r(x)$$ como $$s(x)$$ en $$x=x_0$$.
$$$y_0=r(x_0)=s(x_0) \Rightarrow y_0=r(0)=s(0)=-0+4=4$$$
Por lo tanto el punto de corte entre las rectas $$r$$ y $$s$$ es: $$(x_0=0,y_0=4)$$.
Punto de corte entre $$r$$ y $$t$$:
Se procede igual que en el caso anterior. Igualamos las funciones $$r(x)=-x+4$$ y $$t(x)=x$$ en el punto de corte, que esta vez tendrá por coordenadas $$(x_1,y_1)$$.
$$$ r(x_1)=t(x_1) \Rightarrow -x_1+4=x_1 \Rightarrow x_1=2$$$
Como en el caso anterior, la coordenada $$y$$ del punto de corte, $$y_1$$, es igual al valor que toman las funciones $$r(x)$$ y $$t(x)$$ en el punto de corte:
$$$ y_1=r(x_1)=t(x_1)=-2+4=2$$$
Así pues, las coordenadas del punto de corte son: $$(x_1=2,y_1=2)$$.
Punto de corte entre $$s$$ y $$t$$:
Este punto de corte tendrá por coordenadas $$(x_2,y_2)$$. Primero determinamos el valor de $$x_2$$ como en los casos anteriores, es decir igualando $$s(x)=4$$ y $$t(x)=x$$ en el punto de corte $$x_2$$: $$$ s(x_2)=t(x_2) \Rightarrow 4=x_2 $$$
Se determina el valor de la coordenada $$y$$ del punto de corte, $$y_2$$ como en las anteriores ocasiones: $$$ y_2=s(x_2)=t(x_2)=4 $$$
Por lo tanto el punto de corte entre las rectas $$s(x)$$ y $$t(x)$$ es el que tiene por coordenadas: $$(x_2=4,y_2=4)$$.
Así pues, los vértices de la región de validez tienen por coordenadas: $$$ (x_0,y_0)=(0,4) \quad (x_1,y_1)=(2,2) \quad (x_2,y_2)=(4,4) $$$
Otros ejemplos:
Considerando el sistema de inecuaciones siguiente: $$$ \begin{array}{rcl} x &\geqslant& 0 \\ y &\leqslant& 4 \\ y &\geqslant& \dfrac{x}{2} \end{array}$$$
Buscamos primero las rectas asociadas a cada inecuación y las zonas de validez de cada una:
- La primera de ellas nos da una recta paralela al eje $$y$$ en $$x=0$$ y su región de validez es la que tiene $$x$$ mayor que $$0$$ (hacia la derecha del eje $$y$$).
- La segunda es una recta paralela al eje $$x$$, que pasa por $$y=4$$ y tiene por región de validez el semiplano que tiene por debajo (donde $$y$$ es menor que $$4$$).
- La tercera recta es $$y=\dfrac{x}{2}$$ y su región de validez es la que está por encima de la recta (se puede comprobar facilmente, viendo que el punto $$(0,1)$$ cumple la inecuación: $$1\geqslant$$).
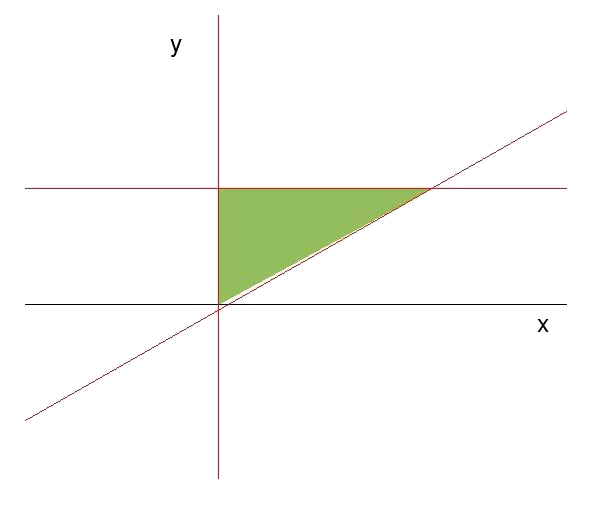
Determinaremos vértices de la zona de validez como los puntos de corte entre las distintas rectas.
- La recta $$x=0$$ corta con $$y=4$$ en el punto $$(x_0=0,y_0=4)$$.
- La recta $$x=0$$ corta con $$y=\dfrac{x}{2}$$ en el punto $$(x_1=0,y_1=0)$$.
- La recta $$y=4$$ corta con $$y=\dfrac{x}{2}$$ en el punto $$(x_2=8,y_2=0)$$.
Por lo tanto, los vértices de la región de validez son: $$$ (x_0,y_0)=(0,4) \quad (x_1,y_1)=(0,0) \quad (x_2,y_2)=(8,0) $$$
Dado el conjunto de restricciones:
$$$ \begin{array}{rcl} x+3 &\geqslant& y \\ 8 &\geqslant& x+y \\ y &\geqslant& x-3 \\ x &\geqslant& 0 \\ y &\geqslant& 0 \end{array}$$$
Buscamos primero las rectas asociadas a cada restricción y las zonas de validez de cada inecuación (comprovando con un punto en las inecuaciones). Las rectas asociadas son:
$$$ \begin{array}{l} f: \ y=3+x \\ g:\ y=-x+8 \\ h:\ y=x-3 \\ i:\ x=0 \\ j:\ y=0 \end{array}$$$
Dibujando las rectas y las zonas de validez podemos visualizar la región de validez.
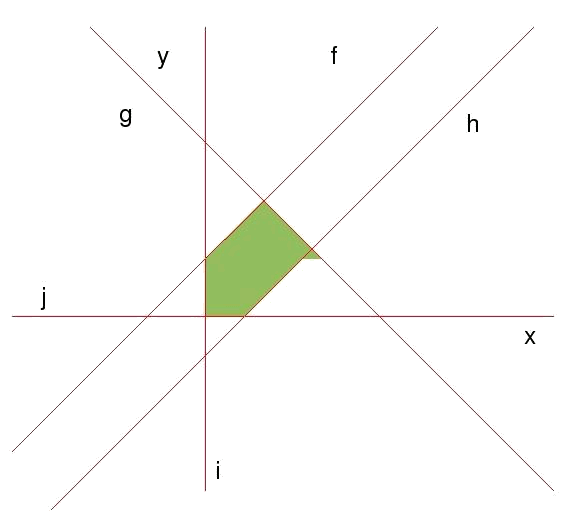
Si no podemos hacer el dibujo tenemos una alternativa. Habiendo tantas rectas, normalmente se tendrán más puntos de corte entre las rectas, que vértices en la zona de validez. Por este motivo ahora no todos los puntos de corte entre las distintas rectas serán vértices de la región de validez. Para reconocer cuáles son los vértices de la región de validez se hará lo siguiente:
-
Se calculan todos los puntos de corte entre las distintas rectas.
- Aquellos puntos de corte en que se cumplan a la vez todas las restricciones serán los vértices de la zona de validez (lo que nos puede permitir visualizarla, si no lo hemos hecho antes).
Procediendo de esta forma con el problema, vamos a calcular todos los puntos de corte entre las distintas rectas:
-
$$f$$ con $$g$$ se cortará en el punto $$(x_0,y_0)$$. Calculamos las coordenadas del punto: $$$f(x_0)=g(x_0) \Rightarrow 3+x_0=-x_0+8 \Rightarrow x_0=\dfrac{5}{2} $$$ Y la coordenada $$y$$: $$$y_0=f(x_0)=g(x_0)=\dfrac{11}{2}$$$ Por lo tanto las coordenadas del punto de corte son: $$(x_0,y_0)=(\dfrac{5}{2}, \dfrac{11}{2})$$.
-
$$f$$ con $$h$$ se cortará en el punto $$(x_1,y_1)$$. Calculamos las coordenadas del punto como ya se ha hecho antes: $$$f(x_1)=h(x_1) \Rightarrow 3+x_1=x_1-3 \Rightarrow 3=-3 $$$ Vemos que al intentar encontrar la coordenada $$x$$ del punto de corte nos aparece una ecuación que no se cumple. Esto quiere decir que las dos rectas son en realidad paralelas (por lo tanto no se cortan nunca).
-
$$f$$ con $$i$$ se cortará en el punto $$(x_2,y_2)$$. La recta $$f(x)=3+x$$ se cortará con la recta $$x=0$$ (recta que coincide con el eje $$y$$) en el punto $$(x=0,y=f(0))$$. Es decir: $$(x_2,y_2)=(0,3)$$.
-
$$f$$ con $$j$$ se cortará en el punto $$(x_3,y_3)$$. Calculamos las coordenadas del punto como ya se ha hecho antes: $$$f(x_3)=j(x_3) \Rightarrow 3+x_3=0 \Rightarrow x_3=-3 $$$ Y la coordenada $$y$$, $$$y_3=f(x_3)=j(x_3)=0$$$ Por lo tanto las coordenadas del punto de corte son: $$(x_3,y_3)=(-3,0)$$.
-
$$g$$ con $$h$$ se cortará en el punto $$(x_4,y_4)$$. Calculamos las coordenadas del punto como ya se ha hecho antes: $$$g(x_4)=h(x_4) \Rightarrow -x_4+8=x_4-3 \Rightarrow x_4=\dfrac{11}{2} $$$ Y la coordenada $$y$$: $$$y_4=g(x_4)=h(x_4)=\dfrac{5}{2}$$$ Por lo tanto las coordenadas del punto de corte son: $$(x_4,y_4)=(\dfrac{11}{2},\dfrac{5}{2})$$.
-
$$g$$ con $$i$$ se cortará en el punto $$(x_5,y_5)$$. La recta $$i$$ nos dice que $$x=0$$, por lo tanto el punto de corte será: $$(0,g(0))=(0,8)$$. Por lo tanto las coordenadas del punto de corte son: $$(x_5,y_5)=(0,8)$$.
-
$$g$$ con $$j$$ se cortará en el punto $$(x_6,y_6)$$. Calculamos las coordenadas del punto como ya se ha hecho antes: $$$ g(x_6)=j(x_6) \Rightarrow -x_6+8=0 \Rightarrow x_6=8 $$$ Y la coordenada $$y$$: $$$y_6=g(x_6)=j(x_6)=0$$$ Por lo tanto las coordenadas del punto de corte son: $$(x_6,y_6)=(8,0)$$.
-
$$h$$ con $$i$$ se cortará en el punto $$(x_7,y_7)$$. La recta $$i$$ nos dice que $$x=0$$, por lo tanto el punto de corte será: $$(0,h(0))=(0,-3)$$. Por lo tanto las coordenadas del punto de corte son:$$(x_7,y_7)=(0,-3)$$.
-
$$h$$ con $$j$$ se cortará en el punto $$(x_8,y_8)$$. Calculamos las coordenadas del punto como ya se ha hecho antes: $$$ h(x_8)=j(x_8) \Rightarrow x_8-3=0 \Rightarrow x_8=3 $$$ Y la coordenada $$y$$: $$$y_8=h(x_8)=j(x_8)=0$$$ Por lo tanto las coordenadas del punto de corte son: $$(x_8,y_8)=(3,8)$$.
- $$i$$ con $$j$$ se cortará en el punto $$(x_9,y_9)$$. La recta $$i$$ nos dice que $$x=0$$, y la $$j$$ que $$y=0$$, por lo tanto las coordenadas del punto de corte son: $$(x_9,y_9)=(0,0)$$.
Determinación de los vértices de la zona de validez:
Se tienen nueve puntos de corte entre las rectas. Como se ha dicho antes, se ha de comprobar en qué puntos se cumplen todas las inecuaciones, y éstos serán los vértices de la región de validez.
$$$ \begin{array}{l} (x_0,y_0)=(\dfrac{5}{2}, \dfrac{11}{2})\ \text{ es compleixen totes les inequacions.} \\ (x_2,y_2)=(0,3)\ \text{ se cumplen todas las inecuaciones.}\\ (x_3,y_3)=(-3,0)\ \text{ no se cumple la inecuación } x\geqslant0. \\ (x_4,y_4)=(\dfrac{11}{2},\dfrac{5}{2})\ \text{ se cumplen todas las inecuaciones.} \\ (x_5,y_5)=(0,8)\ \text{ no se cumple la inecuación } x+3\geqslant y . \\ (x_6,y_6)=(8,0)\ \text{ no se cumple la inecuación } y\geqslant x-3 . \\ (x_7,y_7)=(0,-3)\ \text{ no se cumple la inecuación } y\geqslant 0 . \\ (x_8,y_8)=(3,8)\ \text{ se cumplen todas las inecuaciones.}\\ (x_9,y_9)=(0,0)\ \text{ se cumplen todas las inecuaciones.} \end{array}$$$
Por lo tanto los vértices de la región de validez son: $$$ (x_0,y_0)=(\dfrac{5}{2}, \dfrac{11}{2}) \quad (x_2,y_2)=(0,3)\quad (x_4,y_4)=(\dfrac{11}{2},\dfrac{5}{2})$$$ $$$(x_8,y_8)=(3,8)\quad (x_9,y_9)=(0,0) $$$
En resumen, si se tienen varias inecuaciones simultáneamente, cada una determinará un semiplano donde se cumple. La intersección de estos semiplanos (región conjunta a todos ellos) se le llamará región factible, y es la región en que se cumplen todas las inecuaciones a la vez. Esta zona puede estar acotada o no.
Se determinan los vértices de la zona de validez, determinando los puntos de corte de las rectas de dos en dos. Si se tienen las dos rectas:
$$$f(x)=ax+b \qquad g(x)=cx+d$$$
El punto de corte será $$(x_0,f(x_0))$$ o equivalentemente $$(x_0,g(x_0))$$. Para determinar el punto de corte se hace: $$$ f(x_0)=g(x_0) \Rightarrow ax_0+b=cx_0+d$$$
La solución a esta ecuación es: $$$x_0=\dfrac{d-b}{a-c}$$$
Y las funciones $$f(x)$$ y $$g(x)$$ toman en este punto el valor: $$$f(x_0)=g(x_0)=\dfrac{ad-bc}{a-c}$$$
Siendo pues el punto de corte entre las dos rectas: $$$\Big( x_0=\dfrac{d-b}{a-c}, y_0=\dfrac{ad-bc}{a-c} \Big) $$$
Así se calculan los vértices de la región de validez o región factible.
