Análogamente a la definición de sistema de inecuaciones de una variable, definimos la del sistema de dos variables:
Un sistema de inecuaciones de dos variables es un conjunto de inecuaciones de dos variables que actúan a la vez, es decir, los puntos solución deben cumplir todas las inecuaciones del sistema.
Un ejemplo de sistema de inecuaciones es: $$$ \left\{ \begin{array}{l} y-x+3 < 1 \\ y-x > x-2 \end{array}\right. $$$
Para buscar la solución del sistema, haremos uso principalmente de la definición de sistema de dos variables: buscaremos las soluciones de cada una de las inecuaciones del sistema y a continuación miraremos donde coinciden las regiones soluciones de éstas.
Antes, de buscar dichas regiones, debemos hacer hincapié en el hecho de que en el caso anterior, sistemas de inecuaciones de una variable, era mucho más sencillo intersecar las inecuaciones para encontrar la solución común de todas y por consiguiente la del sistema. En el caso de ahora las soluciones de cada inecuación son regiones en le plano y puede que resulte un poco más complicado encontrar las regiones comunes entre todas las regiones soluciones de cada inecuación del sistema.
Un posible método para encontrar las regiones comunes entre todas las inecuaciones es encontrar primero cada región de cada inecuación y a continuación dibujarse en un mismo plano todas las soluciones juntas, solapándose así las regiones y pudiendo ver fácilmente qué regiones serán solución del sistema.
Volviendo al sistema del ejemplo, vamos a encontrar la solución para mostrar como se debe hacer.
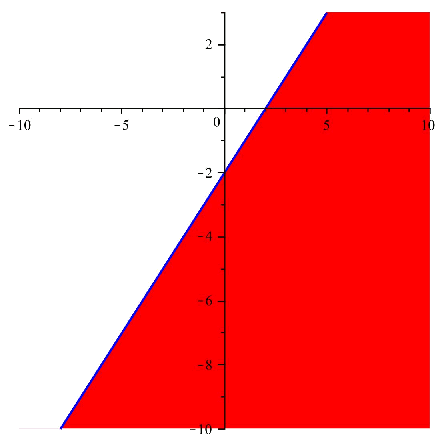
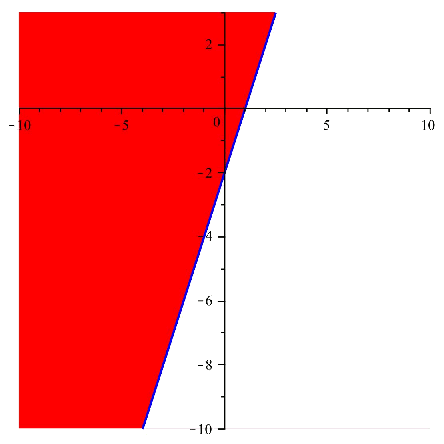
Primero resolvemos las inecuaciones por separado, obteniendo así las soluciones respectivas: $$$ \left\{ \begin{array}{l} y < x-2 \Rightarrow \text{ la región solución es la que está por debajo de la recta} \\ y > 2x-2 \Rightarrow \text{ la región solución es la que está por encima de la recta} \end{array}\right. $$$
A continuación podemos ver estas dos regiones dibujadas en el plano:
Y si superponemos las imágenes, y tomamos la región comun, obtenemos:
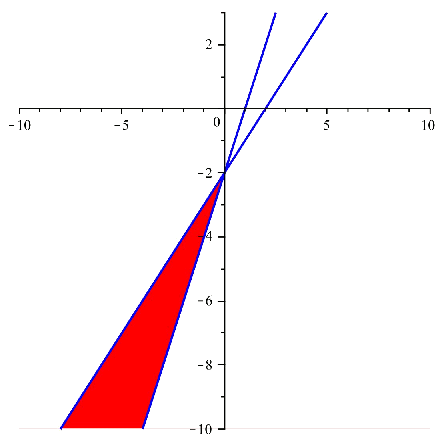
Región solución del sistema:
Esta región simplemente se denota como $$$ \left\{ \begin{array}{l} y < x-2 \\ y > 2x-2 \end{array}\right. $$$ que justamente es la solución de cada uno de las inecuaciones.
En resumen, dado un sistema de inecuaciones, para resolverlo sólo hace falta resolver cada una de las inecuaciones por separado y tomar la región común de entre todas las regiones solución de cada inecuación.
A continuación ponemos algunos ejemplos de casos interesantes de sistemas.
$$$ \left\{ \begin{array}{l} y-x \leqslant 0 \\ x-y \leqslant 0 \end{array}\right. $$$
Resolución: $$$ \left\{ \begin{array}{l} y-x \leqslant 0 \Rightarrow y\leqslant x \\ x-y \leqslant 0 \Rightarrow y\geqslant x \end{array}\right. $$$
En consecuencia la región común es $$y=x$$ y decimos que la solución es la recta $$y=x$$.
$$$ \left\{ \begin{array}{l} 2x-y > 2 \\ -4x +2 > 1 \end{array}\right. $$$
Resolución: $$$ \left\{ \begin{array}{l} 2x-y > 2 \Rightarrow y < 2x-2 \\ -4x +2 > 1 \Rightarrow y > 2x+1 \end{array}\right. $$$
Observamos que las rectas inducidas por las inecuaciones son paralelas y si nos fijamos podemos ver que la siguiente relación $$2x-2 < 2x+1$$ es cierta ya que $$-2 < 1$$ y entonces se cumple $$ y < 2x-2 < 2x+1 < y$$ y nunca encontraremos valores $$x$$ e $$y$$ que hagan cumplir las dos inecuaciones a la vez.
En consecuencia, el sistema es imposible de resolver.
