Los diagramas en árbol son especialmente útiles para resolver problemas con experimentos compuestos, es decir, aquellos donde realizamos más de un experimento aleatorio. Algunos ejemplos de experimentos compuestos son: tirar dos monedas al aire, y mirar si salen dos caras, contar si hay dos mujeres de entre tres hijos, sacar dos bolas de una urna, y mirar si hay una roja y una azul.
Supongamos el siguiente problema:
-
Tiramos tres veces una moneda al aire. Queremos saber la probabilidad del suceso $$A=$$"sacar dos caras".
-
Supongamos ahora que la moneda está descompensada, y $$P(C)=\dfrac{6}{10}, P(+)=\dfrac{4}{10}$$. ¿Cuál es $$P(A)$$ ahora?
- Para resolver el primer problema, podemos aplicar la regla de Laplace, puesto que la probabilidad de que salga cara y salga cruz es la misma en cada lanzamiento de la moneda, $$1/2$$.
Nuestro espacio muestral es $$\Omega=\{CCC,CC+,C+C,C++,+CC,+C+,++C,+++\}$$.
Casos favorables a $$A$$: $$CCC, CC+, C+C, +CC$$. Por lo tanto, $$P(A)=\dfrac{4}{8}=\dfrac{1}{2}$$.
Representemos nuestros resultados en un árbol. Partiendo de la izquierda, en cada tirada dividimos el árbol según si ha salido cara $$(C)$$ o cruz $$(+)$$, poniendo encima de cada rama la probabilidad de que suceda.
En este caso, sale un árbol bastante sencillo.
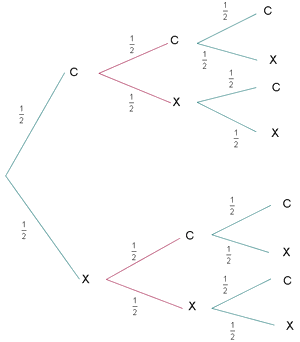
Cada rama del árbol, desde el principio hasta el final, es un resultado del espacio muestral: "primero sale $$C$$, luego $$+$$, y luego $$C$$" corresponde al suceso elemental "$$C+C$$".
Para contar la probabilidad de cada rama, debemos multiplicar las probabilidades de todas las ramas que hemos seguido para llegar hasta el final del árbol (ya que es la probabilidad de la intersección de tres sucesos independientes). Por ejemplo, la probabilidad de $$C+C$$ es $$\dfrac{1}{2}\dfrac{1}{2}\dfrac{1}{2}=\dfrac{1}{8}$$.
Para resolver el problema, debemos sumar las probabilidades de todos los casos favorables. En nuestro caso, cada rama, es decir, cada suceso elemental, tiene probabilidad $$$\dfrac{1}{2}\dfrac{1}{2}\dfrac{1}{2}=\dfrac{1}{8}$$$ y hay cuatro ramas favorables $$$CCC, CC+, C+C, +CC$$$
Por lo tanto, de nuevo encontramos que $$$P(A)=P(CCC)+P(CC+)+P(C+C)+P(+CC)=$$$ $$$=\dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{8}=\dfrac{4}{8}=\dfrac{1}{2}$$$
Una probabilidad del $$50\%$$, el mismo resultado que habíamos encontrado antes. En este caso, el diagrama de árbol no nos ha dicho nada que no supiéramos ya con el teorema de Laplace, pero veamos qué sucede en el apartado siguiente.
-
Ahora la moneda está descompensada, por lo que no podemos aplicar directamente la regla de Laplace. En este caso veremos que utilizar un diagrama de árbol es especialmente útil.
Veamos dibujado nuestro experimento en este caso:
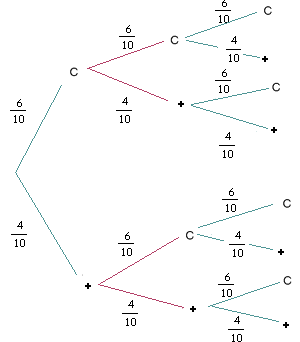
Los casos favorables a $$A$$, son, como antes, $$CCC, CC+, C+C, +CC$$.
$$$P(CCC)=P(C)\cdot P(C) \cdot P(C) = \dfrac{6}{10}\dfrac{6}{10}\dfrac{6}{10}=\dfrac{216}{1000}$$$
$$$P(CC+)=P(C)\cdot P(C) \cdot P(+) = \dfrac{6}{10}\dfrac{6}{10}\dfrac{4}{10}=\dfrac{144}{1000}$$$
$$$P(C+C)=P(C)\cdot P(+) \cdot P(C) = \dfrac{6}{10}\dfrac{4}{10}\dfrac{6}{10}=\dfrac{144}{1000}$$$
$$$P(+CC)=P(+)\cdot P(C) \cdot P(C) = \dfrac{4}{10}\dfrac{6}{10}\dfrac{6}{10}=\dfrac{144}{1000}$$$
Finalmente, $$$P(A) = P(CCC) + P(CC+) + P(C+C) + P(+CC)=$$$ $$$=\dfrac{216}{1000}+\dfrac{144}{1000}+\dfrac{144}{1000}+\dfrac{144}{1000}=\dfrac{648}{1000}=0,648$$$
Es decir, $$A$$ tiene una probabilidad del $$64'8\%.$$
