En este apartado calcularemos áreas determinadas por la gráfica de una función y el eje de las $$x$$. Consideramos una función real $$f(x)$$ y su gráfica $$( x, f(x) )$$ en el plano:
.gif)
Queremos calcular el área coloreada $$A$$. Es decir, el área, $$A$$, determinada por la gráfica de la función, y un cierto intervalo $$[a, b]$$ del eje de las $$x$$, esto es:
$$$A=\int_{a}^b f(x) \ dx$$$
Vamos a calcular el área bajo la función $$f(x)=x^2$$ en el intervalo $$[-2,2]$$. Representemos la función para tener una noción geométrica del problema:
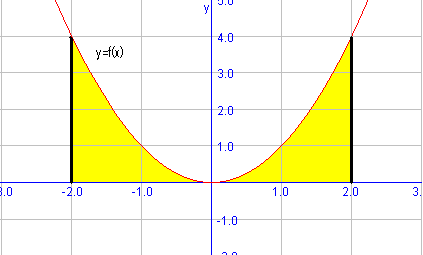
Tenemos pues que integrar la función en el intervalo que delimita el área, o sea: $$$A=\int_{-2}^2 x^2 \ dx=\Big[ \dfrac{x^3}{3} \Big]_{-2}^2= \dfrac{2^3}{3}-\dfrac{(-2)^3}{3}=\dfrac{8}{3}-\dfrac{-8}{3}= \dfrac{16}{3}\mathrm{u}^2$$$
Nota: Cuando escribimos $$u^2$$ nos referimos a las unidades de superficie.
Vamos a calcular el área bajo la función $$f(x)=\sqrt{x}+\sin x$$ en el intervalo $$[0,4]$$. Tal como hemos hecho en el ejemplo anterior, dibujemos primero la función:
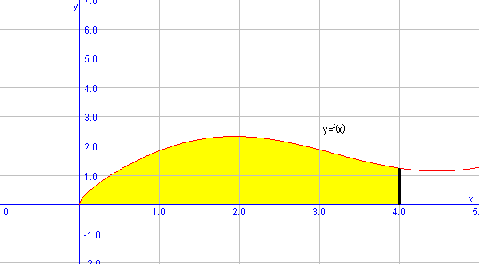
Para calcular el área bajo $$f(x)$$, tenemos que integrar dicha función en el intervalo correspondiente: $$$ \begin{array}{rl} A=&\int_0^4(\sqrt{x}+\sin (x)) \ dx= \int_0^4\sqrt{x} \ dx + \int_0^4\sin(x) \ dx \\ =& \left[ \dfrac{x^{\frac{3}{2}}}{\dfrac{3}{2}} \right]_0^4+ [-\cos(x)]_0^4= \dfrac{2}{3}(8-0)-\cos(4)+1 \\ =& \dfrac{16}{3}+1.65=6.98 u^2 \end{array}$$$
