Concavity and convexity
It is said that a function $$f(x)$$ is convex if, once having joined any two points of the graph, the segment stays over the graph:
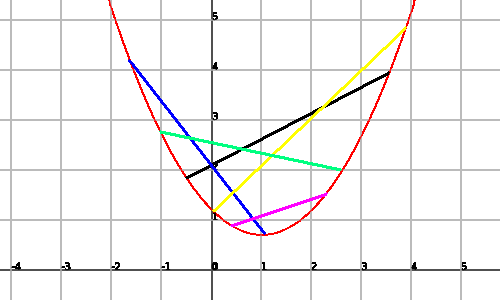
In this graph we can observe different segments (with different colors) that join two points of the graph and stay over it.
An example of a non convex function is:
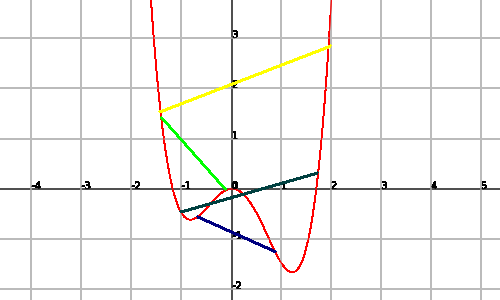since we find segments that join two points of the graph and that are below it.
On the other hand, it is said that a function $$f(x)$$ is concave if the function $$-f(x)$$ is convex, or in other words, if the segments that join the points of the graph $$f(x)$$ are all placed below the graph.
Let's see an example of concave function:
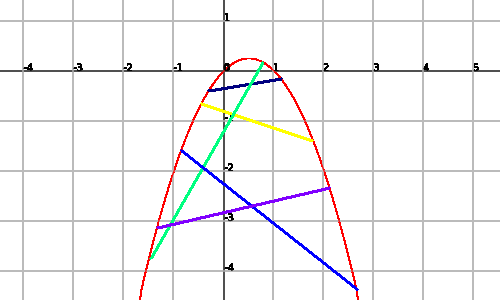
Commonly, we can say that the convex functions are curved functions that are first decreasing and afterwards increasing, while the concave functions are the other way round, they are first increasing and afterwards increasing.
The functions, however, can present concave and convex parts in the same graph, for example, the function $$f(x)=(x+1)^3-3(x+1)^2+2$$ presents concavity in the interval $$(-\infty,0)$$ and convexity in the interval $$(0,\infty)$$:
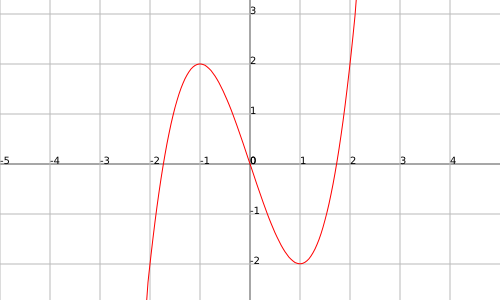
The study of the concavity and convexity is done using the inflection points.
Inflection points
An inflection point is defined as the point in which the function changes from being convex to concave or vice versa.
We can see in the previous example that in the point $$x=0$$ (in the coordinates origin) the function changes from being concave to convex. Therefore we say that $$x=0$$ is an inflection point.
One characteristic of the inflection points is that they are the points where the derivative function has maximums and minimums. Notice that when we approach an inflection point the function increases more every time(or it decreases less), but once having exceeded the inflection point, the function begins increasing less (or decreasing more). This means that in the points where there is an inflection point the derivative will have a maximum or a minimum. Consistently we will find the inflection points by looking for zeros of the second derivative.
We are going to illustrate the process with an example in order to give a simple and clear explanation:
We will consider the function $$f(x)=x^3-3x$$ (it is the function represented in the previous graph).
We can already calculate the maximums and the minimums of the function $$f(x)$$ using the first derivative. The expression of this one is $$f'(x)=3x^2-3$$ and we find maximum and minimum in $$x=-14$$ and $$x=1$$. respectively. If we represent the graph of the derivative we have:
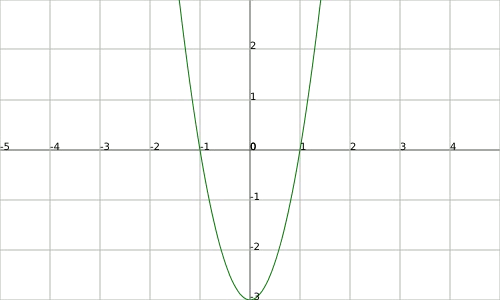
We observe that exactly where the derivative has a minimum is where the function has the inflection point.
To find the point from which we are going to derive the derivative function and equal it to zero: $$$f''(x)=6x \Rightarrow 6x=0 \Rightarrow x=0$$$ and consequently the original function has an inflection point in $$x=0$$.
The process to find the inflection points, the same as finding the maximums and minimums, is an algorithmic and very mechanical process. To derive the function two times, equal it to zero and find the solutions of the equation. These solutions will give us the inflection points.